How To Solve Sudoku
This guide will show you how to solve sudoku puzzles in three steps.
|
|
Sudoku puzzles can be intimidating and difficult to solve, but with a proper strategy, focusing on elimination, you can finish a Sudoku puzzle in mere minutes.
The first step to solving Sudoku puzzles is to try and assign numbers to cells using the 9 big squares. Every number between 1 and 9 must appear once in every big square. There is no real “proper” spot to start a Sudoku puzzle; it is all really up to you. Personally, I like to begin with the centre row. Consider the centre row of the following puzzle (which has been rated at a difficulty of medium):
|
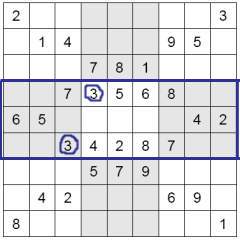 There are two threes in the first two squares. However, there is no three in the last square. Upon further inspection, it can be determined that since the two 3s are in two different rows, it leaves only the empty box in the middle row for the final 3 to fit. If the 3 is placed in any of the other empty cells, there ends up being two 3s in one of the rows. Once you have started, it is not uncommon for a large chain reaction to begin. Using this method you will often be able to solve at least ¼ of a puzzle just with this one step! It’s also quite common for all one number to be found all nine times required, just in this step. Using this method, complete any possible cells in the puzzle. There are two threes in the first two squares. However, there is no three in the last square. Upon further inspection, it can be determined that since the two 3s are in two different rows, it leaves only the empty box in the middle row for the final 3 to fit. If the 3 is placed in any of the other empty cells, there ends up being two 3s in one of the rows. Once you have started, it is not uncommon for a large chain reaction to begin. Using this method you will often be able to solve at least ¼ of a puzzle just with this one step! It’s also quite common for all one number to be found all nine times required, just in this step. Using this method, complete any possible cells in the puzzle.
(In future diagrams, numbers determined using this method will be coloured in blue.)
|
|
The next step involves looking at each of the nine individual squares, and to try and find as many numbers as possible knowing that every number between 1 and 9 can only appear once in every square. After step one, you should have at least one or two squares with only a couple (perhaps two or three) empty cells remaining. It is most definitely worth trying to see if any, and perhaps even all of these squares could somehow be filled in. To do this, I find it is easiest to begin with the box containing the fewest number of empty cells. In our example, after step one, the following numbers are found in the leftmost square of the middle row:
4, 2, 7,
6, 5, 8,
3
|
There are only two cells in this square that do not yet have numbers assigned to them. The numbers missing are 1 and 9. This means one of the two cells will definitely contain a 1, and whichever one remains will contain the 9.
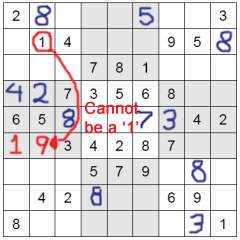 Now to figure out which number goes into which slot. The empty cells are both in the same row, so looking at the numbers in the row do not help us. We are going to solve this by looking at the numbers in the columns in which each cell is located. The column of the first empty cell contains only a 2, a 4, a 6 and an 8. This information cannot help us solve the puzzle, as we need either a 1 or a 9 in either column. The column of the second cell, however, contains an 8, a 1, a 2, a 5 and a 4. Since there is a 1 in this column, the empty cell we are looking at cannot contain a 1, as that would make two 1s in a single column. This means the 9 must fit in that cell, and the 1 fits into the cell next to it. That puzzle is now solved! Here is a diagram displaying the method used to solve this square. Now to figure out which number goes into which slot. The empty cells are both in the same row, so looking at the numbers in the row do not help us. We are going to solve this by looking at the numbers in the columns in which each cell is located. The column of the first empty cell contains only a 2, a 4, a 6 and an 8. This information cannot help us solve the puzzle, as we need either a 1 or a 9 in either column. The column of the second cell, however, contains an 8, a 1, a 2, a 5 and a 4. Since there is a 1 in this column, the empty cell we are looking at cannot contain a 1, as that would make two 1s in a single column. This means the 9 must fit in that cell, and the 1 fits into the cell next to it. That puzzle is now solved! Here is a diagram displaying the method used to solve this square.
|
|
Continue with this method until you have added as many numbers as you can into squares. This step is extremely useful, and, like the previous step, begins a chain reaction. You are most definitely encouraged to use the numbers you have already solved in this step to continue the step. Once this step is completed, the majority of the puzzle should be finished. In fact, if you are lucky and have a good eye, certain puzzles can be finished at the end of this step. In future diagrams, numbers assigned using this method will be coloured in red.
|
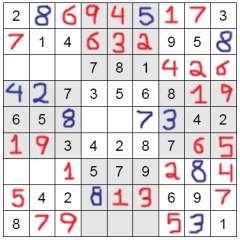 The final step is by very far the easiest, as there should, by now, be almost nothing of the puzzle left to complete. The example puzzle could be completed in step 2, as was mentioned above, but I specifically left certain cells blank in order to be able to demonstrate step 3. Here is how our puzzle looks: The final step is by very far the easiest, as there should, by now, be almost nothing of the puzzle left to complete. The example puzzle could be completed in step 2, as was mentioned above, but I specifically left certain cells blank in order to be able to demonstrate step 3. Here is how our puzzle looks:
As you can tell, it is nearly completed. We are now going to complete the puzzle by filling in the individual rows and columns. Every number between 1 and 9 must fit into each row or column once. Knowing this, we are going to solve the remainder by the process of elimination. Consider the column the furthest to the left. There are two cells remaining, into which the numbers 3 and 9 must fit. The row in which the bottom cell is contains a 9. This means the three must fit into this cell, and the 9 into the top cell. Now we have solved a column!
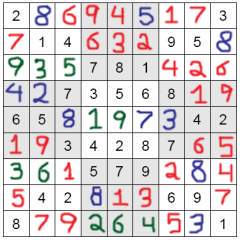 Use this method to complete the puzzle. Once you are finished, you should have something that looks like this: Use this method to complete the puzzle. Once you are finished, you should have something that looks like this:
Congratulations, you have successfully solved a Sudoku puzzle!
|

 There are two threes in the first two squares. However, there is no three in the last square. Upon further inspection, it can be determined that since the two 3s are in two different rows, it leaves only the empty box in the middle row for the final 3 to fit. If the 3 is placed in any of the other empty cells, there ends up being two 3s in one of the rows. Once you have started, it is not uncommon for a large chain reaction to begin. Using this method you will often be able to solve at least ¼ of a puzzle just with this one step! It’s also quite common for all one number to be found all nine times required, just in this step. Using this method, complete any possible cells in the puzzle.
There are two threes in the first two squares. However, there is no three in the last square. Upon further inspection, it can be determined that since the two 3s are in two different rows, it leaves only the empty box in the middle row for the final 3 to fit. If the 3 is placed in any of the other empty cells, there ends up being two 3s in one of the rows. Once you have started, it is not uncommon for a large chain reaction to begin. Using this method you will often be able to solve at least ¼ of a puzzle just with this one step! It’s also quite common for all one number to be found all nine times required, just in this step. Using this method, complete any possible cells in the puzzle. Now to figure out which number goes into which slot. The empty cells are both in the same row, so looking at the numbers in the row do not help us. We are going to solve this by looking at the numbers in the columns in which each cell is located. The column of the first empty cell contains only a 2, a 4, a 6 and an 8. This information cannot help us solve the puzzle, as we need either a 1 or a 9 in either column. The column of the second cell, however, contains an 8, a 1, a 2, a 5 and a 4. Since there is a 1 in this column, the empty cell we are looking at cannot contain a 1, as that would make two 1s in a single column. This means the 9 must fit in that cell, and the 1 fits into the cell next to it. That puzzle is now solved! Here is a diagram displaying the method used to solve this square.
Now to figure out which number goes into which slot. The empty cells are both in the same row, so looking at the numbers in the row do not help us. We are going to solve this by looking at the numbers in the columns in which each cell is located. The column of the first empty cell contains only a 2, a 4, a 6 and an 8. This information cannot help us solve the puzzle, as we need either a 1 or a 9 in either column. The column of the second cell, however, contains an 8, a 1, a 2, a 5 and a 4. Since there is a 1 in this column, the empty cell we are looking at cannot contain a 1, as that would make two 1s in a single column. This means the 9 must fit in that cell, and the 1 fits into the cell next to it. That puzzle is now solved! Here is a diagram displaying the method used to solve this square. The final step is by very far the easiest, as there should, by now, be almost nothing of the puzzle left to complete. The example puzzle could be completed in step 2, as was mentioned above, but I specifically left certain cells blank in order to be able to demonstrate step 3. Here is how our puzzle looks:
The final step is by very far the easiest, as there should, by now, be almost nothing of the puzzle left to complete. The example puzzle could be completed in step 2, as was mentioned above, but I specifically left certain cells blank in order to be able to demonstrate step 3. Here is how our puzzle looks: Use this method to complete the puzzle. Once you are finished, you should have something that looks like this:
Use this method to complete the puzzle. Once you are finished, you should have something that looks like this: